Inverse Trigonometric Functions

Article objectives

To learn about and graph inverse functions.

We will now define those inverse functions, $\boxed{sin^{−1}}$, $\boxed{cos^{−1}}$, and $\boxed{tan^{−1}}$ , and determine their graphs.

f is a function

Recall that a function is a rule that assigns a single object y from one set (the range) to each object x from another set (the domain). We can write that rule as y = f(x), where f is the function (see Figure 1). There is a simple vertical rule for determining whether a rule y = f(x) is a function: f is a function if and only if every vertical line intersects the graph of y = f(x) in the xy-coordinate plane at most once (see Figure 2).

Recall that a function f is one-to-one (often written as 1−1) if it assigns distinct values of y to distinct values of x. In other words, if x₁ $\ne$ x₂ then f(x₁) $\ne$ f(x₂). Equivalently, f is one-to-one if f(x₁) = f(x₂) implies x₁ = x₂. There is a simple horizontal rule for determining whether a function y = f(x) is one-to-one: f is one-to-one if and only if every horizontal line intersects the graph of y = f(x) in the xy-coordinate plane at most once (see Figure 3).

If a function f is one-to-one on its domain, then f has an inverse function, denoted by f⁻¹, such that y = f(x) if and only if f⁻¹(y) = x. The domain of f⁻¹ is the range of f.

The basic idea is that f⁻¹ “undoes” what f does, and vice versa. In other words, f⁻¹(f(x)) = x for all x in the domain of f, and f(f⁻¹(y)) = y for all y in the range of f.

We know from their graphs that none of the trigonometric functions are one-to-one over their entire domains. However, we can restrict those functions to subsets of their domains where they are one-to-one. For example, y = sin x is one-to-one over the interval $\left[−\frac{π}{2}, \frac{π}{2} \right]$, as we see in the graph below:

y = sin x with x restricted to [−π/2, π/2]

For −$\frac{π}{2}$ ≤ x ≤ $\frac{π}{2}$ we have −1 ≤ sin x ≤ 1, so we can define the inverse sine function y = sin⁻¹ x (sometimes called the arc sine and denoted by y = arcsin x) whose domain is the interval [−1,1] and whose range is the interval $\left[−\frac{π}{2}, \frac{π}{2} \right]$. In other words:

$$\text{sin}^{-1}(\text{sin } y) = y \text{ for } −\frac{π}{2} ≤ y ≤ \frac{π}{2}\; \; \; (1)$$ $$\text{sin}(\text{sin}^{-1} x) = x \text{ for } −1 ≤ x ≤ 1 \; \; \; \; (2)$$

Example 1

Find sin⁻¹ $\left(sin \frac{π}{4}\right)$.

Solution: Since $−\frac{π}{2} ≤ \frac{π}{4} ≤ \frac{π}{2}$, we know that sin⁻¹ $\left(sin \frac{π}{4}\right)$ = $\boxed{\frac{π}{4}}$, by formula (1).

Example 2

Find sin⁻¹ $\left(sin \frac{5π}{4}\right)$.

Solution: Since $\frac{5π}{4} > \frac{π}{2}$, we cannot use formula (1). But we know that sin $\frac{5π}{4} = −\frac{1}{\sqrt{2}}$. Thus, sin⁻¹ sin $\left(sin \frac{5π}{4}\right)$ = sin⁻¹ $\left(\frac{1}{\sqrt{2}} \right)$ is, by definition, the angle y such that $−\frac{π}{2} ≤ y ≤ \frac{π}{2}$ and sin y = −$\frac{1}{\sqrt{2}}$. That angle is y = $−\frac{π}{4}$, since

$$sin \left(−\frac{π}{2}\right) = −sin \left(\frac{π}{2}\right) = \frac{1}{\sqrt{2}}$$

Thus, sin⁻¹ $\left(sin \frac{5π}{4}\right) = −\boxed{\frac{π}{4}}$.

Example 2 illustrates an important point: sin⁻¹ x should always be a number between $−\frac{π}{2}$ and $\frac{π}{2}$ . If you get a number outside that range, then you made a mistake somewhere. This why we get sin⁻¹(−0.682) = −43º when using the $\boxed{sin^{−1}}$ button on a calculator. Instead of an angle between 0º and 360º (i.e. 0 to 2π radians) we got an angle between −90º and 90º (i.e. $−\frac{π}{2}$ to $\frac{π}{2}$ radians).

In general, the graph of an inverse function f⁻¹ is the reflection of the graph of f around the line y = x. The graph of y = sin⁻¹ x is shown in Figure 5. Notice the symmetry about the line y = x with the graph of y = sin x.

The inverse cosine function y = cos⁻¹ x (sometimes called the arc cosine and denoted by y = arccos x) can be determined in a similar fashion. The function y = cos x is one-to-one over the interval [0,π], as we see in the graph below:

Thus, y = cos⁻¹ x is a function whose domain is the interval [−1,1] and whose range is the interval [0,π]. In other words:

$$\text{cos}^{-1}(\text{cos } y) = y \text{ for } 0 ≤ y ≤ π \; \; \; \; (3)$$ $$\text{cos}(\text{cos}^{-1} x) = x \text{ for } −1 ≤ x ≤ 1 \; \; \; \; (4)$$

The graph of y = cos⁻¹ x is shown below in Figure 9. Notice the symmetry about the line y = x with the graph of y = cos x.

Example 3

Find cos⁻¹ $\left(cos \frac{π}{3}\right)$.

Solution: Since 0 ≤ $\frac{π}{3}$ ≤ π, we know that cos⁻¹ $\left(cos \frac{π}{3}\right)$ = $\boxed{\frac{π}{3}}$, by formula (3).

Example 4

Find cos⁻¹ $\left(cos \frac{4π}{3}\right)$.

Solution: Since $\frac{4π}{3}$ > π, we cannot use formula (3). But we know that cos $\frac{4π}{3}$ = −$\frac{1}{2}$. Thus, cos⁻¹ $\left(cos \frac{4π}{3}\right)$ = cos⁻¹ $\left(−cos \frac{1}{2}\right)$ is, by definition, the angle y such that 0 ≤ y ≤ π and cos y = −$\frac{1}{2}$. That angle is y = $\frac{2π}{3}$ (i.e. 120º). Thus, $\left(cos \frac{4π}{3}\right)$ = $\frac{2π}{3}$

Examples 2 and 4 may be confusing, since they seem to violate the general rule for inverse functions that f⁻¹(f(x)) = x for all x in the domain of f. But that rule only applies when the function f is one-to-one over its entire domain. We had to restrict the sine and cosine functions to very small subsets of their entire domains in order for those functions to be one-to-one. That general rule, therefore, only holds for x in those small subsets in the case of the inverse sine and inverse cosine.

The inverse tangent function y = tan⁻¹ x (sometimes called the arc tangent and denoted by y = arctan x) can be determined similarly. The function y = tan x is one-to-one over the interval $\left(−\frac{π}{2}, \frac{π}{2} \right)$, as we see in Figure 8:

y = tan with x restricted to [−π/2, π/2]

The graph of y = tan⁻¹ x is shown below in Figure 9. Notice that the vertical asymptotes for y = tan x become horizontal asymptotes for y = tan⁻¹ x. Note also the symmetry about the line y = x with the graph of y = tan x.

Thus, y = tan⁻¹ x is a function whose domain is the set of all real numbers and whose range is the interval $\left(−\frac{π}{2}, \frac{π}{2} \right)$. In other words:

$$\text{tan}^{-1}(\text{tan } y) = y \text{ for } −\frac{π}{2} ≤ y ≤ \frac{π}{2} \; \; \; \; (5)$$ $$\text{tan}(\text{tan}^{-1} x) = x \text{ for } \text{all real }x \; \; \; \; (6)$$

Example 5

Find tan⁻¹ $\left(tan \frac{π}{4}\right)$.

Solution: Since $−\frac{π}{2} ≤ \frac{π}{4} ≤ \frac{π}{2}$, we know that tan⁻¹ $\left(tan \frac{π}{4}\right)$ = $\frac{π}{4}$, by formula (5).

Example 6

Find tan⁻¹ (tan π).

Solution: Since π > $\frac{π}{2}$ , we cannot use formula (5). But we know that tan π = 0. Thus, tan⁻¹ (tan π) = tan⁻¹0 is, by definition, the angle y such that $−\frac{π}{2} ≤ y ≤ \frac{π}{2}$ and tan y = 0. That angle is y = 0. Thus, tan⁻¹ (tan π) = 0 .

Example 7

Find the exact value of $cos\left(sin^{-1} \left(−\frac{1}{4} \right)\right)$.

Solution: Let θ = $sin^{-1} \left(−\frac{1}{4} \right)$. We know that $−\frac{π}{2} ≤ θ ≤ \frac{π}{2}$, so since sin θ = $−\frac{1}{4}$ < 0, θ must be in QIV. Hence cos θ > 0. Thus,

$$cos^2 θ = 1 - sin^2 θ = 1 − \left(−\frac{1}{4} \right)^2 = \frac{15}{16} ⇒ cos θ = \frac{\sqrt{15}}{4}$$

Note that we took the positive square root above since cos θ > 0. Thus, $cos\left(sin^{-1} \left(−\frac{1}{4} \right)\right)$ = $\boxed{\frac{\sqrt{15}}{4}}$.

Example 8

Show that tan (sin⁻¹ x) = $\frac{x}{\sqrt{1 - x^2}}$ for −1 < x < 1.

Solution: When x = 0, the formula holds trivially, since

$$tan (sin^{-1}0) = tan 0 = 0 = \frac{0}{\sqrt{1 - 0^2}} $$

Now suppose that 0 < x < 1. Let θ = sin⁻¹ x. Then θ is in QI and sin θ = x. Draw a right triangle with an angle θ such that the opposite leg has length x and the hypotenuse has length 1, as in Figure 10 (note that this is possible since 0 < x < 1). Then sin θ = $\frac{x}{1}$ = x. By the Pythagorean Theorem, the adjacent leg has length $\sqrt{1 - x^2}$. Thus, tan θ = $\frac{x}{\sqrt{1 - x^2}}$

If −1 < x < 0 then θ = sin⁻¹ x is in QIV. So we can draw the same triangle except that it would be “upside down” and we would again have tan θ = $\frac{x}{\sqrt{1 - x^2}}$, since the tangent and sine have the same sign (negative) in QIV. Thus, tan (sin⁻¹ x) = $\frac{x}{\sqrt{1 - x^2}}$ for −1 < x < 1.

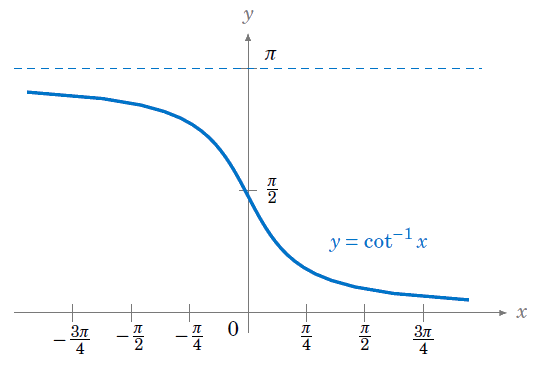
The inverse functions for cotangent, cosecant, and secant can be determined by looking at their graphs. For example, the function y = cot x is one-to-one in the interval (0,π), where it has a range equal to the set of all real numbers. Thus, the inverse cotangent y = cot⁻¹ x is a function whose domain is the set of all real numbers and whose range is the interval (0,π). In other words:

$$\text{cot}^{-1}(\text{cot } y) = y \text{ for } 0 ≤ y ≤ π \; \; \; \; (7)$$ $$\text{cot}(\text{cot}^{-1} x) = x \text{ for } \text{all real }x \; \; \; \; (8)$$

The graph of y = cot⁻¹ x is shown below in Figure 11.

Similarly, it can be shown that the inverse cosecant y = csc⁻¹ x is a function whose domain is |x| ≥ 1 and whose range is $−\frac{π}{2} ≤ y ≤ \frac{π}{2}$, y $\ne$ 0. Likewise, the inverse secant y = sec⁻¹ x is a function whose domain is |x| ≥ 1 and whose range is 0 ≤ y ≤ π, y $\ne \frac{π}{2}$.

$$\text{csc}^{-1}(\text{csc } y) = y \text{ for } −\frac{π}{2} ≤ y ≤ \frac{π}{2}, y \ne 0 \; \; \; \; (9)$$ $$\text{csc}(\text{csc}^{-1} x) = x \text{ for } |x| ≥ 1 \; \; \; \; (10)$$

$$\text{sec}^{-1}(\text{sec } y) = y \text{ for } 0 ≤ y ≤ π, y \ne \frac{π}{2} \; \; \; \; (11)$$ $$\text{sec}(\text{sec}^{-1} x) = x \text{ for } |x| ≥ 1 \; \; \; \; (12)$$

It is also common to call cot⁻¹ x, csc⁻¹ x, and sec⁻¹ x the arc cotangent, arc cosecant, and arc secant, respectively, of x. The graphs of y = csc⁻¹ x and y = sec⁻¹ x are shown in Figure 12:

Example 9

Prove the identity tan⁻¹ x + cot⁻¹ x = $\frac{π}{2}$.

Solution: Let θ = cot⁻¹ x. We have

$$tan \left(\frac{π}{2} − θ\right) = − tan \left(θ − \frac{π}{2}\right) = cot θ = cot(cot^{-1}x) = x $$

by formula (8). So since tan (tan⁻¹ x) = x for all x, this means that tan (tan⁻¹ x) = tan $\left(\frac{π}{2}−θ\right)$. Thus, tan (tan⁻¹ x) = tan ($\frac{π}{2}$ −cot⁻¹ x). Now, we know that 0 < cot⁻¹ x < π, so −$\frac{π}{2}$ < $\frac{π}{2}$ − cot⁻¹ x < $\frac{π}{2}$, i.e. $\frac{π}{2}$ −cot⁻¹ x is in the restricted subset on which the tangent function is one-to-one. Hence, tan (tan⁻¹ x) = tan ($\frac{π}{2}$ −cot⁻¹ x) implies that tan⁻¹ x = $\frac{π}{2}$ −cot⁻¹ x, which proves the identity.

Example 10 Is tan⁻¹ a + tan⁻¹ b = tan⁻¹ $\left(\frac{a + b}{1−ab}\right)$ an identity?

Solution: In the tangent addition formula tan (A +B) = $\frac{tan A + tan B}{1 − tan A tan B}$, let A = tan⁻¹ a and B = tan⁻¹ b. Then

$$tan(tan^{-1}a + tan^{-1}b) = \frac{tan(tan^{-1}a) + tan(tan^{-1}b)}{1 - tan(tan^{-1}a) tan(tan^{-1}b)} $$ $$\frac{a + b}{1 - ab} \text{by formula (6) so it seems that we have}$$ $$tan^{-1}a + tan^{-1}b = tan^{-1}\left(\frac{a + b}{1 - ab} \right)$$

by definition of the inverse tangent. However, recall that −$\frac{π}{2}$ < tan⁻¹ x < $\frac{π}{2}$ for all real numbers x. So in particular, we must have −$\frac{π}{2}$ < tan⁻¹ $\left(\frac{a + b}{1−ab}\right)$ < $\frac{π}{2}$. But it is possible that tan⁻¹ a + tan⁻¹ b is not in the interval ¡ $\left(−\frac{π}{2}, \frac{π}{2}\right)$. For example,

$$tan^{-1}1 + tan^{-1}2 = 1.892547 > \frac{π}{2} ≈ 1.570796 .$$

And we see that $\left(\frac{1 + 2}{1−(1)(2)}\right)$ = tan⁻¹(−3) = −1.249045 $\ne$ tan⁻¹ 1 + tan⁻¹ 2. So the formula is only true when −$\frac{π}{2}$ < tan⁻¹ a + tan⁻¹ b < $\frac{π}{2}$.

Originally ported from <a href="http://www.mecmath.net/trig/" target="_blank">Michael Corral's Trigonometry textbook</a> under the <a href="http://www.gnu.org/copyleft/fdl.html" target="_blank">GNU Free Documentation License, Version 1.3</a> accessed on O by mecmath, used under CC-BY-SA 3.0