Trigonometric Functions of an Acute Angle
Article objectives
Consider a right triangle △ABC, with the right angle at C and with lengths a, b, and c, as in the figure on the right. For the acute angle A, call the leg \(\overline{BC}\) its opposite side, and call the leg \(\overline{AC}\) its adjacent side. The hypotenuse of the triangle is the side \(\overline{AB}\). The ratios of sides of a right triangle occur often enough in practical applications to warrant their own names, so we define the six trigonometric functions of A as follows:

Table 1.2 The six trigonometric functions of A
| Name of function | Abbreviation | Definition |
|---|---|---|
| $$\text{sine} A$$ | $$sin A$$ | $$\frac{\text{opposite side}}{\text{hypotenuse}} = \frac{a}{c}$$ |
| $$\text{cosine} A$$ | $$cos A$$ | $$\frac{\text{adjacent side}}{\text{hypotenuse}} = \frac{b}{c}$$ |
| $$\text{tangent} A$$ | $$tan A$$ | $$\frac{\text{opposite side}}{\text{adjacent side}} = \frac{a}{b}$$ |
| $$\text{cosecant} A$$ | $$csc A$$ | $$\frac{\text{hypotenuse}}{\text{opposite side}} = \frac{c}{a}$$ |
| $$\text{secant} A$$ | $$sec A$$ | $$\frac{\text{hypotenuse}}{\text{adjacent side}} = \frac{c}{b}$$ |
| $$\text{cotangent} A$$ | $$cot A$$ | $$\frac{\text{adjacent side}}{\text{opposite side}} = \frac{b}{a}$$ |
We will usually use the abbreviated names of the functions. Notice from Table 1.2 that the pairs sinA and cscA, cosA and secA, and tanA and cotA are reciprocals:
| $$cscA = \frac{1}{sinA}$$ | $$sec A= \frac{1}{cosA}$$ | $$cotA = \frac{1}{tanA}$$ |
| $$sinA = \frac{1}{cscA}$$ | $$cos A= \frac{1}{secA}$$ | $$tanA = \frac{1}{cotA}$$ |
Example 1

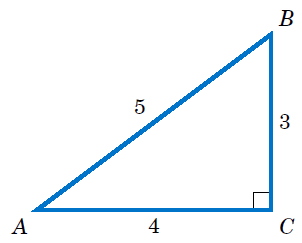
For the right triangle △ABC shown on the right, find the values of all six trigonometric functions of the acute angles A and B.
Solution: The hypotenuse of △ABC has length 5. For angle A, the opposite side \(\overline{BC}\) has length 3 and the adjacent side \(\overline{AC}\) has length 4. Thus:
| $$sinA = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{3}{5}$$ | $$cosA = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{4}{5}$$ | $$tanA = \frac{\text{opposite}}{\text{adjacent}} = \frac{3}{4}$$ |
| $$cscA = \frac{\text{hypotenuse}}{\text{opposite}} = \frac{5}{3}$$ | $$secA = \frac{\text{hypotenuse}}{\text{adjacent}} = \frac{5}{4}$$ | $$cotA = \frac{\text{adjacent}}{\text{opposite}} = \frac{4}{3}$$ |
For angle B, the opposite side \(\overline{AC}\) has length 4 and the adjacent side \(\overline{BC}\) has length 3. Thus:
| $$sinB = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{4}{5}$$ | $$cosB = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{3}{5}$$ | $$tanB = \frac{\text{opposite}}{\text{adjacent}} = \frac{4}{3}$$ |
| $$cscB = \frac{\text{hypotenuse}}{\text{opposite}} = \frac{5}{4}$$ | $$secB = \frac{\text{hypotenuse}}{\text{adjacent}} = \frac{5}{3}$$ | $$cotB = \frac{\text{adjacent}}{\text{opposite}} = \frac{3}{4}$$ |
Notice in Example 1 that we did not specify the units for the lengths. This raises the possibility that our answers depended on a triangle of a specific physical size. For example, suppose that two different students are reading this article: one in the United States and one in Germany. The American student thinks that the lengths 3, 4, and 5 in Example 1 are measured in inches, while the German student thinks that they are measured in centimeters. Since 1 in ≈ 2.54 cm, the students are using triangles of different physical sizes (see Figure 3, 4, 5 below, not drawn to scale).


If the American triangle is △ABC and the German triangle is △A′B′C′, then we see from Figure 3, 4 & 5 that △ABC is similar to △A′B′C′, and hence the corresponding angles are equal and the ratios of the corresponding sides are equal. In fact, you may know that common ratio: the sides of △ABC are approximately 2.54 times longer than the corresponding sides of △A′B′C′. So when the American student calculates sin A and the German student calculates sin A′, they get the same answer:
$$△ABC ∼ △A′B′C′ ⇒ \frac{BC} {B′C′} = \frac{AB} {A′B′} ⇒ \frac{BC} {AB} = \frac{B′C′} {A′B′} ⇒ sin A = sin A′ $$
Likewise, the other values of the trigonometric functions of A and A′ are the same. In fact, our argument was general enough to work with any similar right triangles. This leads us to the following conclusion:
When calculating the trigonometric functions of an acute angle A, you may use any right triangle which has A as one of the angles.
Since we defined the trigonometric functions in terms of ratios of sides, you can think of the units of measurement for those sides as canceling out in those ratios. This means that the values of the trigonometric functions are unitless numbers. So when the American student calculated 3/5 as the value of sin A in Example 1, that is the same as the 3/5 that the German student calculated, despite the different units for the lengths of the sides.
Example 2

Find the values of all six trigonometric functions of 45º.
Solution: Since we may use any right triangle which has 45º as one of the angles, use the simplest one: take a square whose sides are all 1 unit long and divide it in half diagonally, as in the figure on the right. Since the two legs of the triangle △ABC have the same length, △ABC is an isosceles triangle, which means that the angles A and B are equal. So since A +B = 90º, this means that we must have A = B = 45º. By the Pythagorean Theorem, the length c of the hypotenuse is given by
$$c^2 = 1^2 + 1^2 = 2 ⇒ c = \sqrt{2} . $$
Thus, using the angle A we get:
| $$sin45^\circ = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{1}{\sqrt{2}}$$ | $$cos45^\circ = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{1}{\sqrt{2}}$$ | $$tan45^circ = \frac{\text{opposite}}{\text{adjacent}} = \frac{1}{1} = 1$$ |
| $$csc45^\circ = \frac{\text{hypotenuse}}{\text{opposite}} = \sqrt{2}$$ | $$sec45^\circ = \frac{\text{hypotenuse}}{\text{adjacent}} = \sqrt{2}$$ | $$cot45^\circ = \frac{\text{adjacent}}{\text{opposite}} = \frac{1}{1}=1$$ |
Note that we would have obtained the same answers if we had used any right triangle similar to △ABC. For example, if we multiply each side of △ABC by \(\sqrt{2}\), then we would have a similar triangle with legs of length \(\sqrt{2}\) and hypotenuse of length 2. This would give us sin 45º = \(\frac{\sqrt{2}}{2}\) , which equals \(\frac{\sqrt{2}}{\sqrt{2}• \sqrt{2}}\) = \(\frac{1}{\sqrt{2}}\) as before. The same goes for the other functions.
Example 3

Find the values of all six trigonometric functions of 60º.
Solution: Since we may use any right triangle which has 60º as one of the angles, we will use a simple one: take a triangle whose sides are all 2 units long and divide it in half by drawing the bisector from one vertex to the opposite side, as in the figure on the right. Since the original triangle was an equilateral triangle (i.e. all three sides had the same length), its three angles were all the same, namely 60º. Recall from elementary geometry that the bisector from the vertex angle of an equilateral triangle to its opposite side bisects both the vertex angle and the opposite side. So as in the figure on the right, the triangle △ABC has angle A = 60º and angle B = 30º, which forces the angle C to be 90º. Thus, △ABC is a right triangle. We see that the hypotenuse has length c = AB = 2 and the leg \(\overline{AC}\) has length b = AC = 1. By the Pythagorean Theorem, the length a of the leg \(\overline{BC}\) is given by
$$ a^2 + b^2 = c^2 ⇒ a^2 = 2^2 − 1^2 = 3 ⇒ a = \sqrt{3} . $$
Thus, using the angle A we get:
| $$sin60^\circ = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{\sqrt{3}}{2}$$ | $$cos60^\circ = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{1}{2}$$ | $$tan60^\circ = \frac{\text{opposite}}{\text{adjacent}} = \frac{\sqrt{3}}{1} = \sqrt{3}$$ |
| $$csc60^\circ = \frac{\text{hypotenuse}}{\text{opposite}} = \frac{2}{\sqrt{3}}$$ | $$sec60^\circ = \frac{\text{hypotenuse}}{\text{adjacent}} = 2$$ | $$cot60^\circ = \frac{\text{adjacent}}{\text{opposite}} = \frac{1}{\sqrt{3}}$$ |
Notice that, as a bonus, we get the values of all six trigonometric functions of 30º, by using angle B = 30º in the same triangle △ABC above:
| $$sin30^\circ = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{1}{2}$$ | $$cos30^\circ = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{\sqrt{3}}{2}$$ | $$tan30^\circ = \frac{\text{opposite}}{\text{adjacent}} = \frac{1}{\sqrt{3}}$$ |
| $$csc30^\circ = \frac{\text{hypotenuse}}{\text{opposite}} = {2}$$ | $$sec30^\circ = \frac{\text{hypotenuse}}{\text{adjacent}} = \frac{2}{\sqrt{3}}$$ | $$cot30^\circ = \frac{\text{adjacent}}{\text{opposite}} = \frac{\sqrt{3}}{1}$$ |
Example 4

A is an acute angle such that sin A = \(\frac{2}{3}\) . Find the values of the other trigonometric functions of A.
Solution: In general it helps to draw a right triangle to solve problems of this type. The reason is that the trigonometric functions were defined in terms of ratios of sides of a right triangle, and you are given one such function (the sine, in this case) already in terms of a ratio: sin A = \(\frac{2}{3}\) . Since sin A is defined as \(\frac {opposite} {hypotenuse}\) , use 2 as the length of the side opposite A and use 3 as the length of the hypotenuse in a right triangle △ABC (see the figure above), so that sin A = \(\frac{2}{3}\) . The adjacent side to A has unknown length b, but we can use the Pythagorean Theorem to find it:
$$ 2^2 + b^2 = 3^2 ⇒ b^2 = 9 − 4 = 5 ⇒ b =\sqrt{5} $$
We now know the lengths of all sides of the triangle △ABC, so we have:
| $$cosA = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{\sqrt{5}}{3}$$ | $$tanA = \frac{\text{opposite}}{\text{adjacent}} = \frac{2}{\sqrt{5}}$$ |
| $$cscA = \frac{\text{hypotenuse}}{\text{opposite}} = \frac{3}{2}$$ | $$secA = \frac{\text{hypotenuse}}{\text{adjacent}} = \frac{3}{\sqrt{5}}$$ | $$cotA = \frac{\text{adjacent}}{\text{opposite}} = \frac{\sqrt{5}}{2}$$ |
You may have noticed the connections between the sine and cosine, secant and cosecant, and tangent and cotangent of the complementary angles in Examples 1 and 3. Generalizing those examples gives us the following theorem:
Confunction Theorem If A and B are the complementary acute angles in a right triangle △ABC, then the following relations hold:
| $$sin A = cos B$$ | $$sec A = csc B$$ | $$tan A = cot B$$ |
| $$sin B = cos A$$ | $$sec B = csc A$$ | $$tan B = cot A$$ |
We say that the pairs of functions { sin,cos }, { sec,csc }, and { tan,cot } are cofunctions.
So sine and cosine are cofunctions, secant and cosecant are cofunctions, and tangent and cotangent are cofunctions. That is how the functions cosine, cosecant, and cotangent got the “co” in their names. The Cofunction Theorem says that any trigonometric function of an acute angle is equal to its cofunction of the complementary angle.
Example 5
Write each of the following numbers as trigonometric functions of an angle less than 45º: (a) sin 65º; (b) cos 78º; (c) tan 59º.
Solution: (a) The complement of 65º is 90º −65º = 25º and the cofunction of sin is cos, so by the Cofunction Theorem we know that sin 65º = cos 25º. (b) The complement of 78º is 90º −78º = 12º and the cofunction of cos is sin, so cos 78º = sin 12º. (c) The complement of 59º is 90º −59º = 31º and the cofunction of tan is cot, so tan 59º = cot 31º.


The angles 30º, 45º, and 60º arise often in applications. We can use the Pythagorean Theorem to generalize the right triangles in Examples 2 and 3 and see what any 45−45−90 and 30−60−90 right triangles look like, as in Figure 9 & 10 above.
Example 6

Find the sine, cosine, and tangent of 75º.
Solution: Since 75º = 45º+30º, place a 30−60−90 right triangle △ADB with legs of length \(\sqrt{3}\) and 1 on top of the hypotenuse of a 45−45−90 right triangle △ABC whose hypotenuse has length \(\sqrt{3}\), as in the figure on the right. From Figure 9 we know that the length of each leg of △ABC is the length of the hypotenuse divided by \(\sqrt{2}\). So AC = BC = \(\frac{\sqrt{3}}{\sqrt{2}} = \sqrt{\frac{3}{2}}\) . Draw \(\overline{DE}\) perpendicular to \(\overline{AC}\), so that △ADE is a right triangle. Since \(\angle\)BAC = 45º and \(\angle\)DAB = 30º, we see that \(\angle\)DAE = 75º since it is the sum of those two angles. Thus, we need to find the sine, cosine, and tangent of \(\angle\)DAE.
Notice that \(\angle\)ADE = 15º, since it is the complement of \(\angle\)DAE. And \(\angle\)ADB = 60º, since it is the complement of \(\angle\)DAB. Draw \(\overline{BF}\) perpendicular to \(\overline{DE}\), so that △DFB is a right triangle. Then \(\angle\)BDF = 45º, since it is the difference of \(\angle\)ADB = 60º and \(\angle\)ADE = 15º. Also, \(\angle\)DBF = 45º since it is the complement of \(\angle\)BDF. The hypotenuse \(\overline{BD}\) of △DFB has length 1 and △DFB is a 45−45−90 right triangle, so we know that DF = FB = \(\frac{1}{\sqrt{2}}\).
Now, we know that \(\overline{DE} ⊥ \overline{AC} and \overline{BC} ⊥ \overline{AC}\), so \(\overline{FE}\) and \(\overline{BC}\) are parallel. Likewise, \(\overline{FB}\) and \(\overline{EC}\) are both perpendicular to \(\overline{DE}\) and hence \(\overline{FB}\) is parallel to \(\overline{EC}\). Thus, FBCE is a rectangle, since \(\angle\)BCE is a right angle. So EC = FB = \(\frac{1}{\sqrt{2}}\) and FE = BC = \(\sqrt{\frac{3}{ 2}}\) . Hence,
$$DE = DF + FE = \frac{1}{\sqrt{2}} + \sqrt{\frac{3}{ 2}} = \frac{\sqrt{3} + 1}{\sqrt{2}}$$ $$\text{ and AE} = AC − EC = \sqrt{\frac{3}{ 2}} − \frac{1}{\sqrt{2}} = \frac{\sqrt{3} − 1}{\sqrt{2}} .$$
Thus,
$$sin 75^\circ = \frac{DE}{AD} = \frac{\frac{\sqrt{3}+1}{\sqrt{2}}}{2} = \frac{\sqrt{6}+ \sqrt{2}}{ 4} , $$ $$cos 75^\circ = \frac{AE}{AD} = \frac{\frac{\sqrt{3}−1}{\sqrt{2}}}{ 2} = \frac{\sqrt{6}− \sqrt{2}}{ 4} ,$$ $$\text{ and tan } 75^\circ = \frac{DE}{ AE} = \frac{\frac{\sqrt{3}+1}{\sqrt{2}}}{\frac{\sqrt{3}−1}{\sqrt{2}}} = \frac{\sqrt{6}+ \sqrt{2}}{\sqrt{6}− \sqrt{2}}.$$
Note: Taking reciprocals, we get csc 75º = \(\frac{4}{\sqrt{6}+ \sqrt{2}}\), sec 75º = \(\frac{4}{\sqrt{6}− \sqrt{2}}\) , and cot 75º = \(\frac{\sqrt{6}− \sqrt{2}}{\sqrt{6}+ \sqrt{2}}\).